从sklearn开始机器学习 2聚类分类回归和逻辑回归
基本上开始照搬这篇文章了,我可能会做小改动,比如排版什么的或者去其他地方搬运一点,但是先把这个文章贴上。
『行远见大』Python 进阶篇:Sklearn 库
聚类模型
聚类与分类的区别在于聚类不依赖于预先定义的类,没有预定义的类和样本——聚类是一种无监督的数据挖掘任务。
聚类的概念
- 聚类是把各不同的个体分割为有更多相似性子集合的工作
- 聚类生成的子集合称为簇
聚类的要求
- 生成的簇内部的任意两个对象之间具有较高的相似度
- 属于不同簇的两个对象间具有较高的相异度
1 | |
1 | |
1 | |
1 | |
老实讲没太懂这一波调用和评估。有亿点点懵,等我先copy下来再优化 。
1 | |
1 | |
分类模型
常见的分类算法
| 模块名称 | 函数名称 | 算法名称 |
|---|---|---|
| linear_model | LogisticRegression | 逻辑回归 |
| svm | SVC | 支持向量机 |
| neighbors | KNeighborsClassifier | K最近邻居分类 |
| naive_bayes | GaussianNaiveBayes | 高斯朴素贝叶斯 |
| tree | DecisionTreeClassifier | 分类决策树 |
| ensemble | RandomForestClassifier | 随机森林分类 |
| ensemble | GradientBoostingClassifer | 梯度提升分类树 |
因为大佬的算法讲解看起来也很详细,于是就保留了超链接。
构建分类模型
这个案例使用的模型是分类决策树DecisionTreeClassifier.
1 | |
1 | |
参数:
return_X_y : 布尔值,默认为False,如果是True的话,返回(data, target)代替Bunch对象.
返回值:
Bunch对象.类似于字典的对象.其中的属性有:‘data’, the data to learn, ‘target’, the regression targets, and ‘DESCR’, the full description of the dataset.
或者是(data, target) :当return_X_y设为True的时候.
1 | |
1 | |
1 | |
1 | |
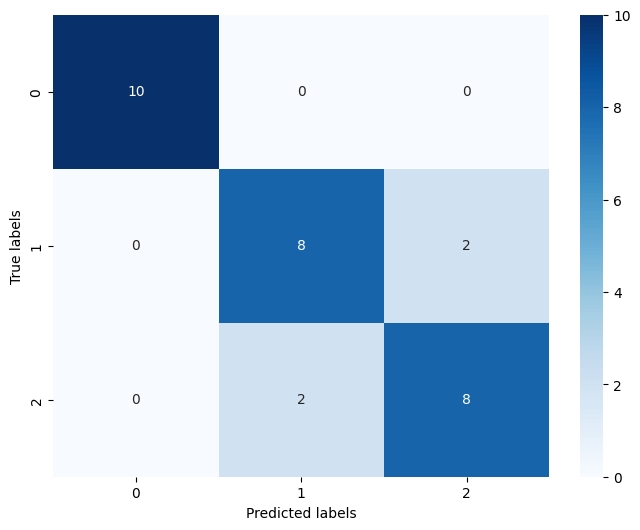
评价分类模型
1 | |
1 | |
1 | |
1 | |
回归模型
常见的回归模型
| 模块名称 | 函数名称 | 算法名称 |
|---|---|---|
| linear_model | LinearRegression | 线性回归 |
| svm | SVC | 支持向量回归 |
| neighbors | KNeighborsRegressor | 最近邻回归 |
| tree | DecisionTreeRegressor | 回归决策树 |
| ensemble | RandomForestRegressor | 随机森林回归 |
| ensemble | GradientBoostingRegressor | 梯度提升回归树 |
构建回归模型
1 | |
1 | |
1 | |
1 | |
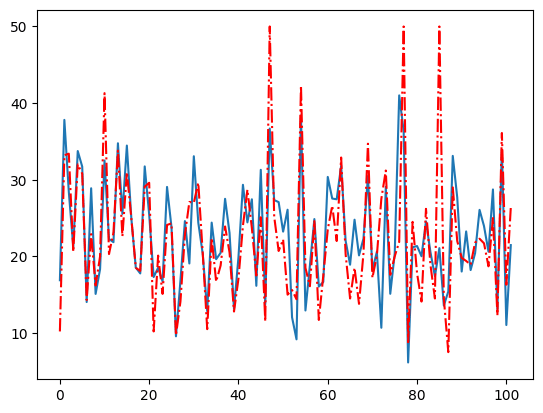
评价回归模型
1 | |
1 | |
1 | |
逻辑回归模型
数据集介绍
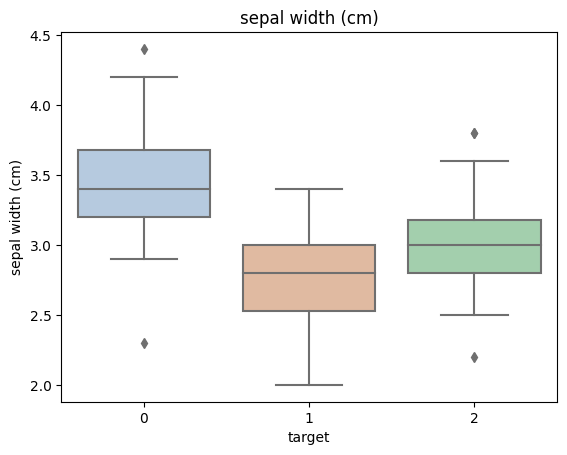
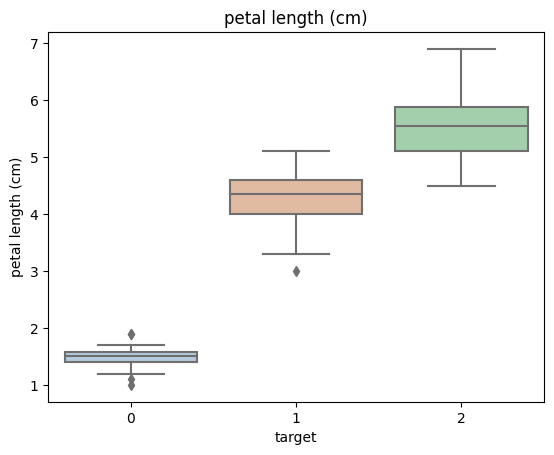
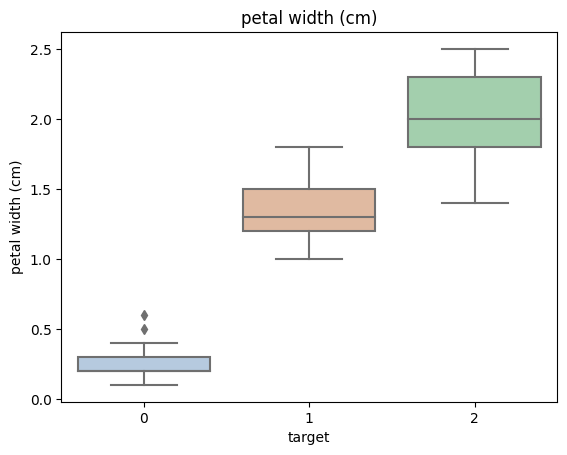
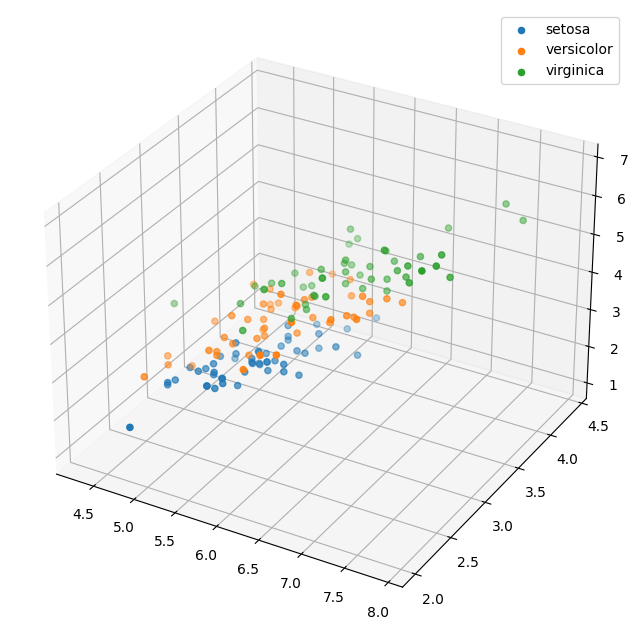
鸢尾花数据(iris)数据集一共有150行数据,每行包含5个变量,其中4个特征变量,1个目标分类变量。
共有150个样本,目标变量为“花的类别”其都属于鸢尾属下的三个亚属,分别是变色鸢尾(Iris-versicolor)、山鸢尾(Iris-setosa)和维吉尼亚鸢尾(Iris-virginica)。
包含的三种鸢尾花的四个特征,分别是花萼长度(sepal length)、花萼宽度(sepal width)、花瓣长度(petal length)、花瓣宽度(petal width)。
任务目标
使用 Sklearn 实现鸢尾花分类,根据鸢尾花的花萼和花瓣大小将其分为三种不同的品种。
配置环境
1 | |
加载数据
1 | |
查看数据
1 | |
1 | |
1 | |
1 | |
1 | |
1 | |
1 | |
1 | |
1 | |
1 | |
1 | |
1 | |
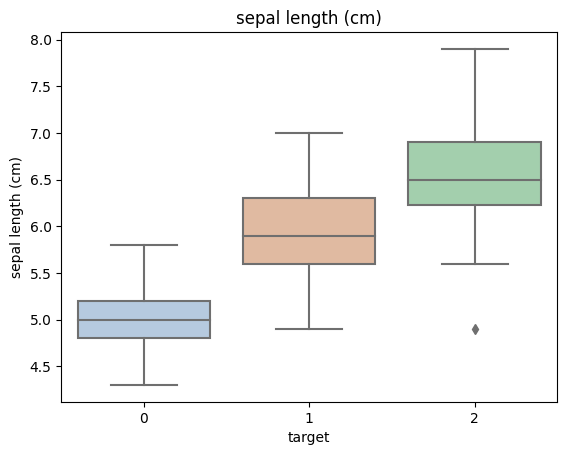
数据可视化
1 | |
1 | |
1 | |
构建二分类逻辑回归模型
1 | |
定义逻辑回归模型
1 | |
1 | |
1 | |
模型预测
1 | |
1 | |

小结:二分类逻辑回归模型的准确度为1,代表所有的样本都预测正确了
构建三分类逻辑回归模型
1 | |
1 | |
由三个参数逻辑回归组合起来即可实现三分类逻辑回归模型
1 | |
1 | |
模型预测
1 | |
1 | |
1 | |
1 | |
1 | |
1 | |